Fattore di correzione del peso nei calcoli della tensione di trazione
Descrive i principi fisici alla base del fattore di correzione del peso (WCF) utilizzato nelle equazioni della tensione di trazione. Mostra l'effetto del fattore di correzione del peso sulla tensione di trazione.
Il fattore di correzione del peso
Nelle equazioni di trazione è presente una costante adimensionale chiamata fattore di correzione del peso (talvolta chiamato fattore di occupazione). Per comprendere il fattore di correzione del peso e le sue implicazioni, diamo prima un’occhiata all’equazione per l’aggiunta di tensione in una sezione rettilinea di condotto.
| Equazione della sezione rettilinea del condotto |
| Tout = Tin + WLwμ |
| Dove: |
| Tout = Tensione in uscita dal tratto rettilineo (lbf, kg, kN) |
| Tin = Tensione di ingresso nel tratto rettilineo (lbf, kg, kN) |
| W = Peso del cavo per unità di lunghezza (lb, kg, kN) |
| w = fattore di correzione del peso (adimensionale) |
| μ = Coefficiente di attrito (COF) (adimensionale) |
Questa equazione mostra che la tensione aggiuntiva da una sezione rettilinea è direttamente proporzionale al peso del cavo, alla lunghezza della sezione, al coefficiente di attrito e al fattore di correzione del peso. Come vedremo, per i tiraggi a cavo singolo, il fattore di correzione del peso (WCF) non influisce sulla tensione perché è uguale a uno (1).
| Contenuti connessi: Rapporto di inceppamento dei cavi |
Tuttavia, per i tiraggi con più di un cavo in un condotto, il WCF è un numero maggiore di 1. Quanto più grande? E su cosa si basa il fattore di correzione del peso?
La teoria alla base del fattore di correzione del peso
Per comprendere la fisica alla base del WCF, si consideri l’esempio di uno o due cavi identici in un condotto.
| Figura 1. Cavo singolo in un condotto |
 |
| Dove: |
| D = Diametro interno (ID) del condotto |
| d = Diametro esterno (OD) del cavo |
| W = Vettore di forza del peso gravitazionale |
| N = Vettore di forza normale |
Nel caso del singolo cavo mostrato nella Figura 1, il cavo non “cade” perché nel punto di contatto con il condotto è presente una forza normale (N) uguale e opposta alla forza del peso gravitazionale (W). Il rapporto tra forza normale e forza gravitazionale è definito come fattore di correzione del peso. Nel caso del singolo cavo, il fattore di correzione del peso è 1 (WCF = 1). Ricorda che è la forza normale moltiplicata per il COF a creare la resistenza di attrito al movimento. Per vincere questa resistenza e spostare il cavo è necessaria una forza di trazione.
| Figura 2. Due cavi identici in un condotto | |
 |
 |
Nel caso di due cavi, vediamo che il punto di contatto si sposta lungo il lato del condotto. Quanto più grandi sono i cavi, tanto più in alto si sposta. La forza normale ora deriva dalla somma vettoriale della forza gravitazionale e di una forza perpendicolare alla forza gravitazionale. La forza normale (l’ipotenusa) è ora maggiore della forza gravitazionale. Il rapporto tra forza normale e forza gravitazionale è il fattore di correzione del peso. All’aumentare del diametro esterno del cavo con un diametro interno del condotto costante, la forza normale aumenta e, per due cavi identici, si avvicina all’infinito quando d → D/2. Tuttavia, un WCF superiore a 2,0 non rappresenta un problema reale nell’installazione dei cavi, a causa delle normative e dei limiti di spazio libero per i cavi.
| Contenuti connessi: Coefficiente di attrito nella trazione dei cavi — Parte 1 |
Equazioni del fattore di correzione del peso
Per il WCF è possibile derivare equazioni (basate su D e d). Queste derivazioni si possono trovare nella letteratura sull’installazione dei cavi. Le equazioni (per 1, 2, 3 e 4 cavi identici) sono:
| Equazioni del fattore di correzione del peso | ||
| |
1 Cavo | |
| |
2 Cavi |  |
| |
3 Cavi (triangolari) |  |
| |
3 cavi (con staffa separatrice) |  |
| |
4 Cavi (rombo) |  |
Analisi del fattore di correzione del peso
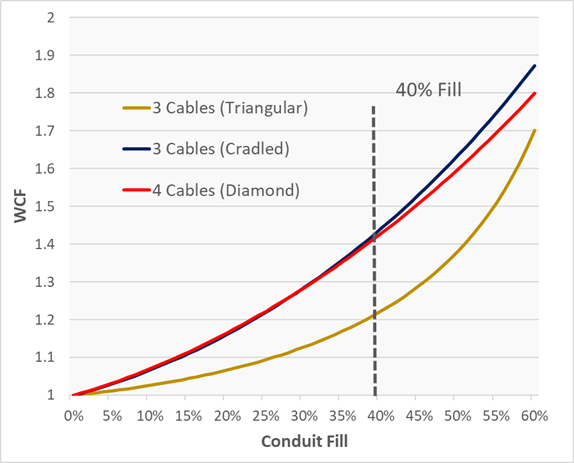
Figura 3 – WCF per varie configurazioni di cavi
La figura 3 rappresenta graficamente il WCF delle tre e quattro equazioni dei cavi in funzione della percentuale di riempimento del condotto. Con i riempimenti tipici dei condotti osserviamo che il WCF varia da 1 a 1,4.
Si noti che tre cavi nella configurazione con separatore mostrano un WCF più elevato rispetto agli stessi tre cavi nella configurazione triangolare. Nei calcoli di trazione, si presume generalmente che tre cavi “rotolino” dalla posizione piatta a quella triangolare una volta che il centro di massa del cavo o dei cavi esterni raggiunge un punto sopra il cavo di base.
| Contenuti connessi: Coefficiente di attrito nella tensione di tiraggio del cavo dalle curve del condotto |
Il WCF per quattro cavi identici nella configurazione a rombo segue da vicino quello di tre cavi in posizione piatta. Ciò non sorprende. Osservando la geometria, notiamo che i punti di contatto per queste configurazioni sono simili.
Gestione del fattore di correzione del peso con Pull-Planner™
Il software Pull-Planner calcola il WCF per 1, 2 e 3 cavi in base al diametro esterno del cavo e all’ID del condotto immessi e alle equazioni di cui sopra. Per 4 o più cavi, o configurazioni complesse con cavi di dimensioni diverse, il software segue l’approccio comune del settore, ovvero impostare WCF su 1,4. Un WCF superiore a 1,4 non è comune nelle normali installazioni di cavi, quindi si tratta di un approccio conservativo. Se è possibile determinare una “configurazione di corsa del cavo” per tiraggi complessi multicavo, solitamente è possibile determinare un WCF. Sebbene questo sia un esercizio che raramente vale la pena fare, Pull-Planner consente all’utente di ignorare il calcolo interno del software e di impostare un WCF quando lo desidera.
Pull-Planner “srotola” i cavi dalla posizione piatta a quella triangolare con un rapporto prudente D/d <= 2,5 (riempimento del 48%). Ciò significa che i tiraggi a tre cavi con un riempimento inferiore al 40% vengono calcolati con la configurazione piatta, a meno che i cavi non siano triplexati.
| Contenuti connessi: Domande frequenti: tiraggio, lubrificazione e tensione dei cavi |
Il punto effettivo in cui tre cavi potrebbero passare a una configurazione triangolare dipende non solo dalle dimensioni del cavo, ma anche dalla configurazione dell’alimentazione, dall’esistenza di curve opposte che fanno sì che i cavi attraversino il condotto e dalla distribuzione della forza di trazione sui cavi. Se è garantita una configurazione triangolare, l’utente può ignorare WCF come descritto sopra.
Implicazioni del fattore di correzione del peso nei calcoli della tensione di trazione
Abbiamo dimostrato che il WCF nel calcolo di una sezione rettilinea è lineare. Solitamente aggiunge una tensione aggiuntiva dal 20% al 40% per i tiraggi di più cavi. Ciò si aggiungerebbe ovviamente al peso maggiore del fascio di cavi (due o tre cavi anziché uno).
E cosa succede nelle curve dei condotti?
| Equazione della curva del condotto (semplificata*) |
| Tout = Tin * ewμϴ |
| Dove: |
| Tout = tensione in uscita dalla curva (lbf, kg, kN) |
| Tin = tensione di ingresso nella curva (lbf, kg, kN) |
| w = fattore di correzione del peso (adimensionale) |
| μ = Coefficiente di attrito (COF) (adimensionale) |
| ϴ= Angolo di curvatura (radianti) |
| e = Base del logaritmo naperiano (costante) |
Si noti che in una curva di un condotto il WCF è un esponente di un moltiplicatore. Inserendo il tipico intervallo WCF, la tensione in uscita da una curva aumenta dal 5% al 15%.
Teoria e realtà
L’analisi di cui sopra è teorica. Polywater® ha eseguito test di trazione confrontando il tiraggio di un singolo cavo con quello di più cavi. L’esistenza e l’entità di qualsiasi WCF possono essere determinate confrontando i risultati della tensione misurata. Presentare quei dati richiederà un altro post sul blog, ma per i curiosi, la correlazione è piuttosto buona. Lasciate il WCF nei vostri calcoli!
Hai qualche domanda?
* L’equazione di curvatura semplificata è un’approssimazione piuttosto accurata quando le tensioni in entrata sono molto maggiori del peso del cavo nella curva.
