Modell und Analyse des Rohrverschiebungsfaktors beim Einziehen von Glasfaserkabeln – Die Auswirkung des Reibungskoeffizienten auf das Modell der Rohrverschiebung
In diesem Artikel zeigen wir Ihnen, wie sich der Reibungskoeffizient (COF) auf die Kabelspannung auswirkt, wenn das Kabel durch Wellungen oder regelmäßige Verschiebungen in Rohren gezogen wird.

Die durch den Memory-Effekt der Abwicklung bedingten Verschiebungen in Endlosrohren mit Glasfaserkabeln wurden modelliert, wie in Abbildung 1 dargestellt. Die Verschiebung des Rohres wird als eine „sich wiederholende Welle“ behandelt, die entlang der Länge des Rohres verläuft, mit einer „Amplitude (A)“ und einer „Periode (P)“. Teil 1 dieser Serie beschreibt die Theorie hinter diesem Modell. Teil 2 dieser Serie zeigt, wie wir den Winkel berechnen können, der (pro Längeneinheit) durch die regelmäßigen Verschiebungen entsteht. Anschließend können die Kabelzug-Gleichungen verwendet werden, um die Zugspannung auf der Grundlage des Gesamtwinkels bei einem Kabel-Einzug abzuschätzen. In diesem Teil 3 wird gezeigt, wie sich der Reibungskoeffizient (COF) auf die Kabelspannung auswirkt, wenn das Kabel durch Wellungen oder regelmäßige Verschiebungen in Rohren gezogen wird.
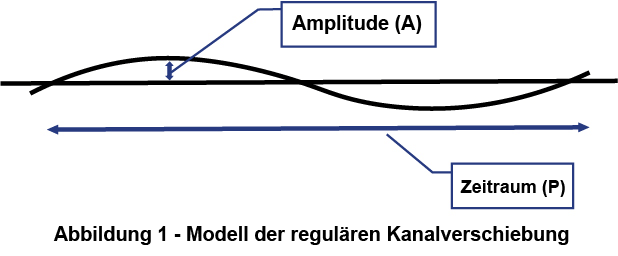
ABBILDUNG 1. Modell der regelmäßigen Rohrverschiebung
In früheren Artikeln wurden die Auswirkungen von Amplituden- und Periodenschwankungen auf den Krümmungswinkel und die Zugspannung aufgezeigt. Die Analyse zeigt, dass die Krümmung bei der Verschiebung deutlich unter 1,6 Grad pro Meter gehalten werden muss, um lange Glasfaserkabel-Einzüge (Tausende von Metern) mit sicheren Zugspannungen durchzuführen.
| Verwandte Inhalte: Modell und Analyse des Rohrverschiebungsfaktors beim Einziehen von Glasfaserkabeln – Teil 1 |
Die Auswirkung der Reibung im Modell
Wir wissen, dass die Reibung, gemessen als „Reibungskoeffizient“ (COF), eine wichtige Variable für die Zugspannung ist. In einem geraden Rohrabschnitt ist die Zugspannung direkt proportional zum Reibungskoeffizienten. Wenn wir also den Reibungskoeffizienten verdoppeln, verdoppeln wir die Zugspannung. Umgekehrt können wir bei einer Halbierung des Reibungskoeffizienten mit der gleichen Zugkraft doppelt so weit ziehen.
Wie verhält es sich mit Veränderungen der Reibung bei der kontinuierlichen Verschiebung dieses Modells?
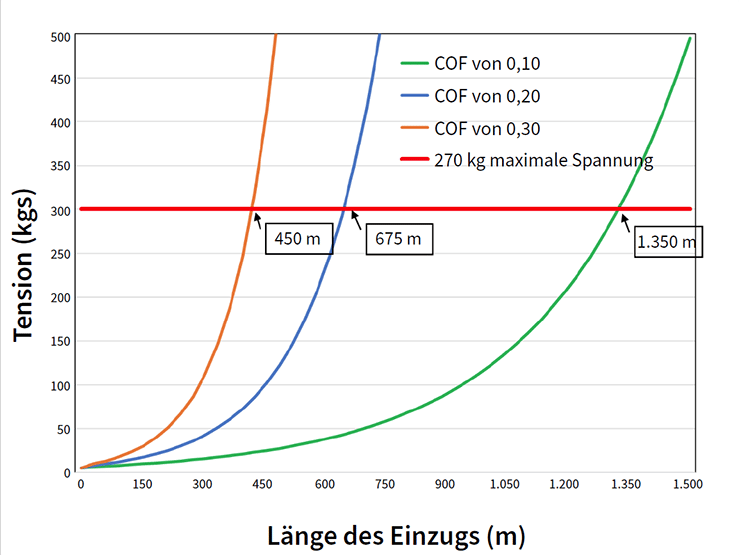
ABBILDUNG 2. Spannung vs. Zuglänge (Verschiebungswinkel = 1,6°/m)
Abbildung 2 zeigt den Verlauf der Spannung im Verhältnis zur Entfernung bei einem Glasfaserkabel-Einzug. Der Verschiebungswinkel wurde auf 1,6 Grad pro Meter eingestellt. Bei den Berechnungen wird ein Kabelgewicht von 150 g/m und eine anfängliche Eingangsspannung von 45 N angenommen. Es werden drei Reibungskoeffizienten berechnet (COF = 0,10, COF = 0,20 und COF = 0,30), die einen typischen Reibungsbereich auf der Grundlage von Feld- und Labormessungen darstellen.
Das Diagramm zeigt, wie wichtig es ist, die Reibung zu minimieren. Mit der gleichen Spannung kann man dreimal so weit einziehen, wenn der Reibungskoeffizient um den Faktor drei reduziert wird. Die Entfernung, die ein Kabel mit einer bestimmten Spannung eingezogen werden kann, ist umgekehrt proportional zum Reibungskoeffizienten, ebenso wie bei der Berechnung eines geraden Abschnitts. Das Diagramm schätzt 270 kg. Spannung bei 1.350 Meter, 675 Meter und 4,5 Meter mit Reibungskoeffizienten von 0,10, 0,20 bzw. 0,30.
| Verwandte Inhalte: So vermeiden Sie das Quetschen von Glasfaserkabeln bei der Installation |
Die Theorie
Diese Linearität ist etwas überraschend, wenn wir uns die vereinfachte Form (eine Annäherung*) der Kabelzug-Gleichung für eine Krümmung ansehen (Gleichung 1). Die Reibung ist in einem Exponenten, der üblicherweise keine Linearität impliziert.
Rohrkrümmung Tout = Tin eμϴ
Wobei:
Tout = Spannung am Ende
Tin = Spannung am Anfang
μ = Reibungskoeffizient
ϴ = Krümmungswinkel (Bogenmaß)
e = Natürliche Logarithmusbasis
Bei näherer Betrachtung zeigt sich jedoch, dass, wenn „Spannung am Ende“ und „Spannung am Anfang“ konstant sind, auch der Faktor eμϴ konstant bleiben muss. Veränderungen von μ (COF) müssen mit reziproken Veränderungen von ϴ ausgeglichen werden. Mit anderen Worten: Höhere Krümmungswinkel können durch einen niedrigeren Reibungskoeffizienten ausgeglichen werden.
ϴ ist jedoch der Gesamt-Krümmungswinkel, den wir wie folgt beschreiben können:
ϴ = φ * d (Gleichung 2)
Wobei:
Θ = Gesamt-Krümmungswinkel
φ = Verschiebungswinkel pro Länge (1,6 Grad/m in Abbildung 2)
d = Zuglänge oder Gesamtlänge.
Wenn wir also μ verdoppeln, muss die Länge halbiert werden, um den Gesamtwinkel um den Faktor 2 zu verringern. Die umgekehrte Proportionalität ergibt sich daraus, dass sich die Gesamtkrümmung proportional zur Länge im Modell ergibt.
In früheren Artikeln wurde gezeigt, dass der Rohr-Verschiebungswinkel je nach Positionierung des Rohres um eine Größenordnung variieren kann (von 0,2° bis 2,0°). Gleichung 1 bekräftigt, wie wichtig es ist, den Verschiebungswinkel zu minimieren. Es ist einfach nicht möglich, die Auswirkungen größerer Verschiebungen durch geringere Reibung auszugleichen.
| Verwandte Inhalte: Die Ursprünge der Schmierung beim Einblasen von Kabeln: Ein Interview mit dem Experten Willem Griffioen |
Anfangsspannung
Schließlich zeigt Gleichung 1, wie wichtig die minimale Anfangsspannung ist. Wenn sich die Anfangsspannung verdoppelt, verdoppelt sich auch die Spannung. Die Zuglänge bei einer bestimmten Spannung wird ebenfalls erheblich reduziert.
Berechnungshilfe verfügbar
Wenn Sie daran interessiert sind, die in dieser Analyse verwendeten Berechnungshilfe (Excel) zu erhalten, füllen Sie bitte das nachstehende Formular „E-Mail“ aus. Einer unserer Techniker wird Ihnen die Berechnungshilfe zusenden und sich mit Ihnen in Verbindung setzen, um Ihnen die Details der Dateneingabe zu erläutern.
*Die Annäherung in Gleichung 1 ist relativ genau, wenn die Spannungen am Anfang wesentlich höher sind als das Gewicht des Kabels in der Krümmung. Für die vom Verschiebungsmodell vorhergesagten Krümmungen mit großem Radius wurde jedoch die vollständige Gleichung (mit Gewichtskomponente) zur Diagrammberechnung verwendet Diese Gleichungen sagen eine höhere Spannung voraus als die Annäherung, insbesondere wenn die eingehende Spannung gegen Null geht.